Hello JAX！ • Lumin Space

角色	库/工具	职责
引擎/计算	JAX	负责底层的矩阵运算、求导、编译 (替代`torch.Tensor`+`autograd`)
神经网络	Flax	负责定义层、模型结构 (替代`torch.nn`)
优化器	Optax	负责 Adam, SGD 等优化算法 (替代`torch.optim`)
数据加载	PyTorch	没错！即使是 JAX 教程，也建议继续用`torch.utils.data.DataLoader`，因为这块 PyTorch 做得最好，而且数据加载不需要 GPU 加速。

为什么我要自找麻烦学 JAX？

快
看懂 JAX 相关代码

PyTorch (动态图) ：采用即时执行（Eager Execution） 模式。系统逐行解析代码并单独调度每个算子到 GPU，由于缺乏对后续操作的全局视野，无法进行跨算子的统筹优化，导致原本可并行的计算往往被串行执行，增加了显存访问和内核启动的开销。

JAX (JIT 编译) ：采用即时编译（JIT Compilation） 技术。系统通过追踪（Tracing）构建完整的静态计算图，利用 XLA 编译器进行算子融合（Operator Fusion） 和指令重排。这使得系统能提前规划最优执行路径，减少显存读写次数并充分利用硬件的并行计算能力。

为了获得这个速度，你必须遵守 JAX 的“清规戒律” 。这也是为什么 JAX 难上手的原因。

限制一：No Side-Effects
- PyTorch/Python 习惯：你可以在函数里悄悄修改全局变量，或者修改输入的列表。
- JAX 规矩：函数只能通过 return 返回结果，不能悄悄改东西。
- 典型禁忌：In-place 操作。
  - ❌ x[0] = 1 （原地修改，JAX 禁止）
  - ✅ y = x.at[0].set(1) （创建一个新的 x，把值改了赋给 y）
限制二：Static Shapes
- 解释：编译器（JIT）在编译时需要知道张量的具体形状。
- 典型禁忌：y = x[x > 3]。
  - 因为 x 里有多少个大于 3 的数是不确定的，这会导致 y 的长度忽长忽短，编译器会疯掉。

JAX as NumPy on accelerators#

DeviceArray 与异步调度 (Asynchronous Dispatch)#

数据结构：DeviceArray

定义：JAX 的核心数据结构是 jaxlib.xla_extension.DeviceArray（在较新版本中统一为 jax.Array）。
内存驻留：与 NumPy 的 ndarray 默认驻留内存不同，JAX 的 Array 默认直接分配在加速器显存（GPU/TPU）中。

互操作性：

jax.numpy (jnp) 尽可能复刻了 numpy (np) 的 API。
JAX 可以在计算中混合使用 NumPy 数组和 JAX 数组。当两者运算时，JAX 会隐式触发 Host-to-Device 的数据传输，将 NumPy 数组搬运至 GPU，结果返回为 DeviceArray。
显式传输控制：
- jax.device_put(x): Host $\rightarrow$ Device
- jax.device_get(x): Device $\rightarrow$ Host

import jax
import jax.numpy as jnp
print("Using jax", jax.__version__)
a = jnp.zeros((2, 5), dtype=jnp.float32)
print(a)
b = jnp.arange(6)
print(b)
# [0 1 2 3 4 5]
b.__class__
# jaxlib.xla_extension.DeviceArray
b.device()
# GpuDevice(id=0, process_index=0)
b_cpu = jax.device_get(b)
print(b_cpu.__class__)
# <class 'numpy.ndarray'>
b_gpu = jax.device_put(b_cpu)
print(f'Device put: {b_gpu.__class__} on {b_gpu.device()}')
# Device put: <class 'jaxlib.xla_extension.DeviceArray'> on gpu:0
b_cpu + b_gpu
# DeviceArray([ 0,  2,  4,  6,  8, 10], dtype=int32)
jax.devices()
# [GpuDevice(id=0, process_index=0), GpuDevice(id=1, process_index=0)]

python

执行机制：异步调度 (Asynchronous Dispatch)

这是一个非常关键的性能特性。

现象：当你执行 c = jnp.matmul(a, b) 时，Python 解释器会立即返回一个 c 的句柄（Future），而不会等待 GPU 计算完成。
原理：JAX 维护了一个指令队列。Python 线程只需将操作压入队列即可继续向下执行。这意味着 Python 代码的执行通常领先于 GPU 的实际计算。
同步点 (Blocking) ：只有当你试图读取结果的具体数值时（例如 print(c)、np.array(c) 或控制流判断 if c > 0），JAX 才会强制阻塞 Python 线程，等待 GPU 计算完成并传回数据。
意义：这最大化了 CPU（指令分发）和 GPU（大规模并行计算）的重叠执行时间，隐藏了 Python 的解释器开销。

不可变张量 (Immutable Tensors)#

范式约束

JAX 约束：JAX 数组是不可变 (Immutable) 的。
NumPy 对比：NumPy 支持 In-place 更新，即 x[0] = 1 会直接修改内存地址中的值。
JAX 行为：x[0] = 1 在 JAX 中会抛出 TypeError。

原因：函数式编程与追踪 (Tracing)

JAX 的核心能力依赖于对纯函数（Pure Functions）的追踪（Tracing）来构建计算图（Jaxpr）。

如果允许 In-place 修改，会引入副作用 (Side Effects) ，使得输入变量的状态在函数执行过程中发生改变。这会导致编译器（XLA）难以分析数据依赖关系，从而使得梯度计算和算子融合变得极度复杂甚至不可行。

y = x.at[0].set(1)
# x 保持原值
# y 是新值
b_new = b.at[0].set(1)
print('Original array:', b)
print('Changed array:', b_new)
# Original array: [0 1 2 3 4 5]
# Changed array: [1 1 2 3 4 5]

python

编译优化：你可能会担心这就意味着大量的显存拷贝（Copy overhead）。但在 jax.jit 编译后，XLA 编译器足够智能，它会分析数据流。如果原数组 x 在后续不再被使用，XLA 会在底层的 GPU Kernel 中将其优化为原地修改 (In-place mutation) 。因此，这种写法在编译后的性能与原地修改是一致的。

无状态伪随机数生成 (Stateless PRNG)#

传统模式：有状态 (Stateful)

NumPy/PyTorch：维护一个全局的随机数生成器状态（Global Context）。
操作：调用 torch.randn() 时，函数内部会隐式地读取并更新这个全局状态。
问题：这种隐式的状态更新违背了“纯函数”原则。在并行计算或分布式训练中，隐式状态会导致随机数序列难以复现，且难以进行并行的独立采样。

JAX 模式：无状态 (Stateless)

核心原则：随机数生成是一个确定性的函数： $Output = f(Key, Structure)$ 。只要 Key 不变，生成的随机数永远不变。
PRNG Key：你必须显式地创建和传递随机数状态（Key）。

key = jax.random.PRNGKey(42)

python

关键操作：Split

为了在生成随机数的同时获得下一个可用的状态，JAX 引入了 split 机制。

单次使用原则：一个 Key 只能用于一次随机采样操作（或者说，同一个 Key 用于同一操作会得到完全相同的结果）。
Split 流程：将一个旧的 Key 分裂为多个新的、统计学上独立的 Key。

rng, subkey = jax.random.split(rng)
# subkey -> 用于当前的随机操作 (如 dropout, init weights)
# rng    -> 传递给后续的代码块继续 split

python

图示逻辑：

Key_t \xrightarrow{\text{split}} (Key_{t+1}, SubKey_{task})

你总是保留一个主 Key (rng) 用于向下传递，而“消耗”掉分裂出来的 subkey 用于具体的计算任务。

rng = jax.random.PRNGKey(42)
# A non-desirable way of generating pseudo-random numbers...
jax_random_number_1 = jax.random.normal(rng)
jax_random_number_2 = jax.random.normal(rng)
print('JAX - Random number 1:', jax_random_number_1)
print('JAX - Random number 2:', jax_random_number_2)

# Typical random numbers in NumPy
np.random.seed(42)
np_random_number_1 = np.random.normal()
np_random_number_2 = np.random.normal()
print('NumPy - Random number 1:', np_random_number_1)
print('NumPy - Random number 2:', np_random_number_2)

python

JAX - Random number 1: -0.18471177
JAX - Random number 2: -0.18471177
NumPy - Random number 1: 0.4967141530112327
NumPy - Random number 2: -0.13826430117118466

rng, subkey1, subkey2 = jax.random.split(rng, num=3)  # We create 3 new keys
jax_random_number_1 = jax.random.normal(subkey1)
jax_random_number_2 = jax.random.normal(subkey2)
print('JAX new - Random number 1:', jax_random_number_1)
print('JAX new - Random number 2:', jax_random_number_2)

python

JAX new - Random number 1: 0.107961535
JAX new - Random number 2: -1.2226542

‍

Function transformations with Jaxpr#

JAX 不仅仅是一个数值计算库，更是一个编译器前端。它通过一种称为 Tracing（追踪） 的机制，将 Python 函数转换为一种中间表示（Intermediate Representation, IR），即 Jaxpr (JAX Expression) 。基于这个 IR，JAX 实现了自动微分、编译优化等功能。

中间表示：Jaxpr (JAX Expression)#

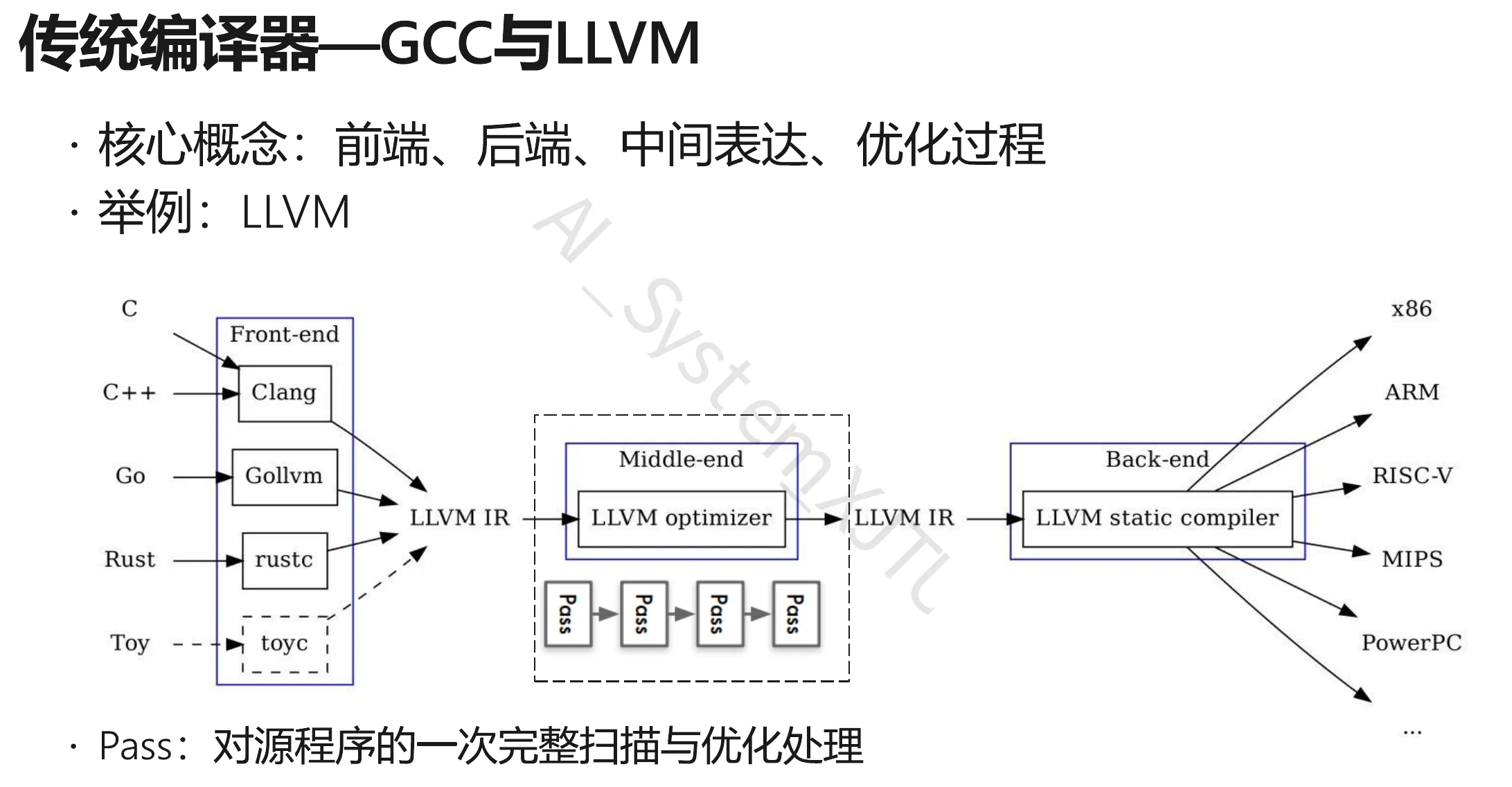
左侧 (Frontend) ：有 $M$ 种源语言 (C, C++, Go, Rust…)。
右侧 (Backend) ：有 $N$ 种硬件架构 (x86, ARM, RISC-V…)。
中间 (IR) ：只有 1 种核心表达 (LLVM IR)。

如果没有 IR,你需要为每一对“语言-硬件”写一个编译器（比如 C-to-x86, Go-to-ARM）。你需要写 $M \times N$ 个编译器。这是一场工程灾难。

有了 IR：

前端只需负责将源码翻译成 IR ( $M$ 个前端)。
后端只需负责将 IR 翻译成机器码 ( $N$ 个后端)。
复杂度降低：从 $M \times N$ 降到了 $M + N$ 。

映射到 JAX：

Frontend: Python (用户写的高级代码)。
IR: Jaxpr (以及更底层的 XLA HLO)。
Backend: NVIDIA GPU, Google TPU, CPU。
意义：JAX 不需要专门为 GPU 写一套 Python 解释器，也不用为 TPU 写另一套。它只需要把 Python 变成 Jaxpr，剩下的交给 XLA 编译器（后端）去处理如何搬运到不同硬件上。

Jaxpr vs. LLVM IR：不同层级的抽象

LLVM IR (通用计算的 IR)

抽象对象：寄存器、内存地址、基础算术指令（加减乘除）、跳转指令。
设计目标：优化标量计算、控制流（if/else/loop）。
图示对应：图中中间框内的 “LLVM IR”。

Jaxpr (深度学习的 IR)

抽象对象：张量 (Tensors) 、高阶算子 (MatMul, Conv)、自动微分原语。
设计目标：保留数据流结构，方便进行数学变换（微分）和大规模并行化。
本质：Jaxpr 是一种 Domain Specific IR (DSIR) 。

关键区别：

如果你在 LLVM IR 层面做“自动微分”，会极其痛苦，因为那里只有寄存器和指针，丢失了“矩阵乘法”这样的数学语义。

而在 Jaxpr 层面，系统清楚地知道 dot_general 是矩阵乘法，因此可以轻松应用 $\frac{\partial (WX)}{\partial W} = X^T$ 这样的数学规则。

Optimization Passes (优化遍)

图片中间有一个核心模块：LLVM Optimizer 和下面的 Pass -> Pass -> Pass。

什么是 Pass？ Pass 是编译器对 IR 进行的一次完整扫描和变换。每次 Pass 都在不改变程序语义的前提下，让代码变得更高效。

在 LLVM 中：

Dead Code Elimination Pass: 删除永远不会执行的代码。
Loop Unrolling Pass: 把循环展开。

在 JAX (基于 Jaxpr/XLA) 中： 当你调用 @jax.jit 时，JAX 会生成 Jaxpr，然后 XLA 编译器会对这个 IR 执行一系列针对深度学习的 Pass：

Operator Fusion Pass (算子融合) ：
- 输入 IR: Load A -> Load B -> Add -> Store Temp -> Load Temp -> Relu -> Store C
- 优化后 IR: Load A, B -> Add & Relu -> Store C (融合为一个 Kernel，消灭中间内存读写)。
Buffer Donation Pass:
- 分析 IR 中的变量生命周期，复用显存，减少内存申请开销。
CSE (Common Subexpression Elimination) :
- 发现 IR 里算了两次一样的 a * b，改成只算一次。

‍ 请记住公式 $y = \frac{1}{|x|} \sum_{i} \left[ (x_i + 2)^2 + 3 \right]$ ，后面代码都源于它。

def simple_graph(x):
    x = x + 2
    x = x ** 2
    x = x + 3
    y = x.mean()
    return y

inp = jnp.arange(3, dtype=jnp.float32)
print('Input', inp)
print('Output', simple_graph(inp))
# Input [0. 1. 2.]
# Output 12.666667
jax.make_jaxpr(simple_graph)(inp)
'''
{ lambda ; a:f32[3]. let
    b:f32[3] = add a 2.0
    c:f32[3] = integer_pow[y=2] b
    d:f32[3] = add c 3.0
    e:f32[] = reduce_sum[axes=(0,)] d  //沿着维度0规范求和
    f:f32[] = div e 3.0  //除以3
  in (f,) }
'''

python

A jaxpr representation follows the structure:

jaxpr ::= { lambda Var* ; Var+.
            let Eqn*
            in  [Expr+] }

plaintext

纯函数约束 (Purity Constraint)

教程中的 norm(x) 示例展示了非纯函数（Impure Function）在 Tracing 机制下的行为：

代码：global_list.append(x)
现象：生成的 Jaxpr 中完全丢失了这一行操作。
原因：list.append 是 Python 的副作用操作，不属于 JAX 的原语。Tracer 在追踪过程中虽然执行了这行 Python 代码，但因为没有产生 JAX 的数据依赖，这个操作不会被记录在计算图中。
结论：JAX 变换只对数据流 (Data Flow)敏感，对 Python 的控制流 (Control Flow)和副作用 (Side Effects) 只有在它们直接影响 JAX 数组计算时才会被捕捉（控制流需要用 jax.lax.cond 等原语替代）。

global_list = []

# Invalid function with side-effect
def norm(x):
    global_list.append(x)
    x = x ** 2
    n = x.sum()
    n = jnp.sqrt(n)
    return n

jax.make_jaxpr(norm)(inp)
'''
{ lambda ; a:f32[3]. let
    b:f32[3] = integer_pow[y=2] a
    c:f32[] = reduce_sum[axes=(0,)] b
    d:f32[] = sqrt c
  in (d,) }
'''

python

Automatic differentiation#

变换映射：jax.grad 是一个高阶函数，其映射关系为：

f: \mathbb{R}^n \rightarrow \mathbb{R} \implies \nabla f: \mathbb{R}^n \rightarrow \mathbb{R}^n

输入原函数，返回梯度函数。(grad输出的每一维对应那个向量的偏导数)

grad_function = jax.grad(simple_graph)
gradients = grad_function(inp)
print('Gradient', gradients)

python

原函数： $y = \frac{1}{3} \sum ((x+2)^2 + 3)$

根据链式法则（Chain Rule）：

\frac{\partial y}{\partial x} = \underbrace{\frac{\partial y}{\partial \text{sum}}}_{\text{Mean的导数}} \cdot \underbrace{\frac{\partial \text{sum}}{\partial \text{square}}}_{\text{Sum的导数}} \cdot \underbrace{\frac{\partial \text{square}}{\partial (x+2)}}_{\text{Square的导数}}

{ lambda ; a:f32[3]. let

b:f32[3] = add a 2.0

c:f32[3] = integer_pow[y=2] b

d:f32[3] = integer_pow[y=1] b

e:f32[3] = mul 2.0 d

f:f32[3] = add c 3.0

g:f32[] = reduce_sum[axes=(0,)] f

_:f32[] = div g 3.0

h:f32[] = div 1.0 3.0

i:f32[3] = broadcast_in_dim[broadcast_dimensions=() shape=(3,)] h

j:f32[3] = mul i e

in (j,) }

‍

为了计算梯度，往往需要用到前向传播的中间值。

b:f32[3] = add a 2.0: 计算 $x+2$ 。
c:f32[3] = integer_pow[y=2] b: 计算 $(x+2)^2$ 。
f:f32[3] = add c 3.0: 计算 $(x+2)^2 + 3$ 。

‍

这里对应数学中的 $\frac{d}{dx}(u^2) = 2u$ 。

d:f32[3] = integer_pow[y=1] b:
- 这是计算 $b^1$ ，也就是 $x+2$ 本身。
- 为什么会有这行？ 因为幂函数的求导通用公式是 $n \cdot u^{n-1}$ 。这里 $n=2$ ，所以它是算 $u^{2-1}$ 。
e:f32[3] = mul 2.0 d:
- 这是计算 $2.0 \times d$ 。
- 结论：e 现在的数值就是 $2(x+2)$ 。这是 $(x+2)^2$ 这一层的局部梯度。

‍

g:f32[] = reduce_sum[axes=(0,)] f: 对前向结果求和。
_:f32[] = div g 3.0: 求平均值。
- 注意变量名 _ ：在 Python 和很多 IR 中，下划线表示“我不关心这个结果”。
- 因为你调用的是 jax.grad 而不是 jax.value_and_grad，你只想要梯度。虽然为了追踪图结构，JAX 生成了计算 Loss 的步骤，但它并未将其作为最终输出返回。

‍

h:f32[] = div 1.0 3.0:
- 计算标量 $1.0 / 3.0 = 0.333...$ 。这就是 $\frac{1}{N}$ 。
i:f32[3] = broadcast_in_dim[... shape=(3,)] h:
- 广播 (Broadcast) ：将标量 $0.333$ 复制扩展成一个长度为 3 的向量 [0.333, 0.333, 0.333]。
- 这代表了 Loss 对求和层之前的每一个元素的梯度权重都是 $1/3$ 。

‍

j:f32[3] = mul i e:
- i 是 Mean 层的梯度 ( $\frac{1}{3}$ ).
- e 是 Square 层的梯度 ( $2(x+2)$ ).
- 它们相乘： $\frac{1}{3} \times 2(x+2) = \frac{2}{3}(x+2)$ 。

‍

Jaxpr 实际上是在执行以下数学运算：

\nabla = \left( \underbrace{\text{broadcast}(\frac{1}{3})}_{i} \right) \times \left( \underbrace{2 \cdot (x+2)}_{e} \right)

JAX 的工作流：它通过 Trace 拿到了计算图，然后应用微积分规则（Adjoint Logic），生成了一个新的计算图（就是你看到的这个 Jaxpr）来专门计算梯度。

Value and Grad

API: jax.value_and_grad(f)
目的：在深度学习训练中，我们通常需要同时获取 Loss 值（用于日志记录）和 Gradients（用于参数更新）。
效率：该函数通过一次前向传播和一次反向传播同时计算 $f(x)$ 和 $\nabla f(x)$ ，避免了分别调用 f(x) 和 jax.grad(f)(x) 导致的重复前向计算开销。

val_grad_function = jax.value_and_grad(simple_graph)
val_grad_function(inp)

"""
(DeviceArray(12.666667, dtype=float32),
 DeviceArray([1.3333334, 2.       , 2.6666667], dtype=float32))
"""

python

PyTrees

定义：JAX 将嵌套的容器结构（如 dict of list of arrays）称为 PyTree。
应用：神经网络的参数通常以字典形式组织（如 {'layer1': {'w': ..., 'b': ...}}）。jax.grad 能够自动处理这种结构，返回一个与输入参数结构完全一致的梯度 PyTree。

Just-In-Time Compilation#

XLA (Accelerated Linear Algebra)

jax.jit 是连接 JAX 前端与 XLA 后端的桥梁。

流程：Python Function $\xrightarrow{\text{Trace}}$ Jaxpr $\xrightarrow{\text{Lowering}}$ HLO (High Level Optimizer) IR $\xrightarrow{\text{Compile}}$ Optimized Kernel (Machine Code)。
算子融合 (Kernel Fusion) ：这是 XLA 带来的最大性能收益。它将多个内存密集型操作（如 add, mul）融合为一个 GPU Kernel，极大减少了 HBM（高带宽内存）的读写次数。

多态性与重编译 (Polymorphism & Re-compilation)

静态形状限制：编译后的 Kernel 是针对特定输入形状（Input Shape）硬编码的。
触发机制：
1. 第一次调用 jitted_function 时，触发 Tracing 和 Compilation（耗时较长）。
2. 后续调用若输入形状相同，直接调用缓存的 Kernel（极快）。
3. 若输入形状改变，JAX 必须重新编译。因此，在处理变长序列（如 NLP）时，通常需要使用 Padding 将输入固定为标准长度，以避免频繁的重编译开销。

由于 JAX 的异步调度机制，Python 端的计时器会在指令分发完成后立即停止，而不是等待 GPU 计算结束。

解决方案：在测速时必须调用 .block_until_ready()，强制同步 CPU 和 GPU，以获取真实的执行时间。
结果分析：截图显示，JIT 编译后的函数比原 Python 函数快了约 10-15倍（ $598\mu s$ vs $19.5\mu s$ ），且梯度计算的加速效果更为显著。

jitted_function = jax.jit(simple_graph)
# Create a new random subkey for generating new random values
rng, normal_rng = jax.random.split(rng)
large_input = jax.random.normal(normal_rng, (1000,))
# Run the jitted function once to start compilation
_ = jitted_function(large_input)

%%timeit
simple_graph(large_input).block_until_ready()
# 598 µs ± 104 µs per loop (mean ± std. dev. of 7 runs, 1 loop each)
%%timeit
jitted_function(large_input).block_until_ready()
# 19.5 µs ± 52.8 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

python

‍

Implementing a Neural Network with Flax#

The Model#

有状态 vs 无状态 (The Mental Model Shift)

这是这一节最让 PyTorch 用户“抓狂”的地方，必须首先建立这个概念：

PyTorch (torch.nn.Module ) : 是有状态的 (Stateful) 。
- 当你实例化 model = Net() 时，model 对象内部持有了所有的权重（Weights）和偏置（Biases）。
- 你调用 model(x) 时，它自动使用内部存的权重。
Flax (flax.linen.Module ) : 是无状态的 (Stateless) 。
- Flax 的 model 对象仅仅是代码逻辑的容器（或者说是“蓝图”），它不存储任何参数数据。
- 参数（Params）必须单独存放在一个字典里。
- 你不能直接调用 model(x)，你必须显式地把参数传进去：model.apply(params, x)。

from flax import linen as nn

class MyModule(nn.Module):
    # Some dataclass attributes, like hidden dimension, number of layers, etc. of the form:
    # varname : vartype
    hidden_dim： int

    def setup(self):
        # Flax uses "lazy" initialization. This function is called once before you
        # call the model, or try to access attributes. In here, define your submodules etc.
        pass

    def __call__(self, x):
        # Function for performing the calculation of the module.
        pass

python

类属性
1. 你不需要写 __init__ 来接收超参数。你只需要像写变量类型声明一样写在类里，Flax 会自动为你生成一个 __init__ 函数。
2. 当你实例化时，直接写 model = MyModule(hidden_dim=128) 即可。
惰性初始化
1. 在 PyTorch 中，__init__ 是在对象创建那一刻执行的。
2. 在 Flax 中，setup 不是在 model = MyModule(...) 时执行的。它是在你第一次调用 model.init 或 model.apply 的时候，才会被“惰性”调用的。
3. 为什么？ 因为 JAX 需要等待输入数据进来，推断出数据的 Shape，才能确定权重的形状（比如全连接层的输入维度），从而完成初始化。
__call__(self, x) 方法 —— 对应 PyTorch 的 forward

‍

class SimpleClassifier(nn.Module):
    num_hidden : int   # Number of hidden neurons
    num_outputs : int  # Number of output neurons

    def setup(self):
        # Create the modules we need to build the network
        # nn.Dense is a linear layer
        self.linear1 = nn.Dense(features=self.num_hidden)
        self.linear2 = nn.Dense(features=self.num_outputs)

    def __call__(self, x):
        # Perform the calculation of the model to determine the prediction
        x = self.linear1(x)
        x = nn.tanh(x)
        x = self.linear2(x)
        return x

class SimpleClassifierCompact(nn.Module):
    num_hidden : int   # Number of hidden neurons
    num_outputs : int  # Number of output neurons

    @nn.compact  # Tells Flax to look for defined submodules
    def __call__(self, x):
        # Perform the calculation of the model to determine the prediction
        # while defining necessary layers
        x = nn.Dense(features=self.num_hidden)(x)
        x = nn.tanh(x)
        x = nn.Dense(features=self.num_outputs)(x)
        return x

model = SimpleClassifier(num_hidden=8, num_outputs=1)\
print(model)
'''
SimpleClassifier(
    # attributes
    num_hidden = 8
    num_outputs = 1
)
'''

rng, inp_rng, init_rng = jax.random.split(rng, 3)
inp = jax.random.normal(inp_rng, (8, 2))  # Batch size 8, input size 2

# Initialize the model
params = model.init(init_rng, inp)
print(params)
'''
FrozenDict({
    params: {
        linear1: {
            kernel: DeviceArray([[ 0.31476864, -0.4647768 , -0.7862042 , -0.48842615,
                          -0.65373844,  0.3892545 ,  0.3038056 ,  0.04179859],
                         [-0.3298236 ,  1.1110363 ,  0.54909396, -0.8168818 ,
                           0.40057245, -0.8665987 ,  1.2087964 ,  1.0364622 ]],            dtype=float32),
            bias: DeviceArray([0., 0., 0., 0., 0., 0., 0., 0.], dtype=float32),
        },
        linear2: {
            kernel: DeviceArray([[-0.27971813],
                         [-0.7466775 ],
                         [ 0.29791608],
                         [-0.26267236],
                         [-0.5084385 ],
                         [ 0.04573093],
                         [-0.47257012],
                         [ 0.50458497]], dtype=float32),
            bias: DeviceArray([0.], dtype=float32),
        },
    },
})
'''

model.apply(params, inp)
'''
DeviceArray([[-0.48368204],
             [ 0.04365474],
             [ 0.06668529],
             [-0.34203646],
             [ 0.4835147 ],
             [ 0.37424874],
             [ 0.14232653],
             [-0.5916512 ]], dtype=float32)
'''

python

‍

The Data#

直接使用pytorch便好，但是有一些细节需要注意：

唯一的微小区别：

在 generate_continuous_xor 函数里，作者使用了 numpy.random 而不是 torch.randn。这是为了保证随机数生成的逻辑和 JAX 之前的章节保持一致（显式种子控制），也为了避免引入不必要的 torch.Tensor 依赖。数据是以 pure NumPy array 的形式存储的。

The Data Loader Class (关键的胶水代码)

这里有一个关键的技术细节：Collate Function。

默认情况下，PyTorch 的 DataLoader 会把一堆数据 stack 起来，然后自动转换为 torch.Tensor。但在 JAX 的训练循环里，我们需要的是 NumPy Array（或者是 JAX Array）。

所以，我们需要覆盖默认的转换逻辑def numpy_collate。

import torch.utils.data as data

class XORDataset(data.Dataset):

    def __init__(self, size, seed, std=0.1):
        """
        Inputs:
            size - Number of data points we want to generate
            seed - The seed to use to create the PRNG state with which we want to generate the data points
            std - Standard deviation of the noise (see generate_continuous_xor function)
        """
        super().__init__()
        self.size = size
        self.np_rng = np.random.RandomState(seed=seed)
        self.std = std
        self.generate_continuous_xor()

    def generate_continuous_xor(self):
        # Each data point in the XOR dataset has two variables, x and y, that can be either 0 or 1
        # The label is their XOR combination, i.e. 1 if only x or only y is 1 while the other is 0.
        # If x=y, the label is 0.
        data = self.np_rng.randint(low=0, high=2, size=(self.size, 2)).astype(np.float32)
        label = (data.sum(axis=1) == 1).astype(np.int32)
        # To make it slightly more challenging, we add a bit of gaussian noise to the data points.
        data += self.np_rng.normal(loc=0.0, scale=self.std, size=data.shape)

        self.data = data
        self.label = label

    def __len__(self):
        # Number of data point we have. Alternatively self.data.shape[0], or self.label.shape[0]
        return self.size

    def __getitem__(self, idx):
        # Return the idx-th data point of the dataset
        # If we have multiple things to return (data point and label), we can return them as tuple
        data_point = self.data[idx]
        data_label = self.label[idx]
        return data_point, data_label

dataset = XORDataset(size=200, seed=42)
print("Size of dataset:", len(dataset))
print("Data point 0:", dataset[0])

# This collate function is taken from the JAX tutorial with PyTorch Data Loading
# https://jax.readthedocs.io/en/latest/notebooks/Neural_Network_and_Data_Loading.html
def numpy_collate(batch):
    if isinstance(batch[0], np.ndarray):
        return np.stack(batch)
    elif isinstance(batch[0], (tuple,list)):
        transposed = zip(*batch)
        return [numpy_collate(samples) for samples in transposed]
    else:
        return np.array(batch)

data_loader = data.DataLoader(dataset, batch_size=8, shuffle=True, collate_fn=numpy_collate)

# next(iter(...)) catches the first batch of the data loader
# If shuffle is True, this will return a different batch every time we run this cell
# For iterating over the whole dataset, we can simple use "for batch in data_loader: ..."
data_inputs, data_labels = next(iter(data_loader))

# The shape of the outputs are [batch_size, d_1,...,d_N] where d_1,...,d_N are the
# dimensions of the data point returned from the dataset class
print("Data inputs", data_inputs.shape, "\n", data_inputs)
print("Data labels", data_labels.shape, "\n", data_labels)

python

Data inputs (8, 2)
[[ 1.0504987 1.0865755 ]
[ 0.02809919 -0.06226995]
[ 0.06141667 1.0757508 ]
[ 0.08356921 -0.11297069]
[ 1.0324166 -0.01301431]
[ 1.0024511 0.04979983]
[ 0.3078881 0.11195749]
[ 1.0371146 0.9396015 ]]
Data labels (8,)
[0 0 1 0 1 1 0 0]

Optimization#

两个新概念：Optax（优化器库）和 TrainState（训练状态容器）。

import optax
# Input to the optimizer are optimizer settings like learning rate
optimizer = optax.sgd(learning_rate=0.1)
from flax.training import train_state
model_state = train_state.TrainState.create(apply_fn=model.apply,
                                            params=params,
                                            tx=optimizer)

python

PyTorch: optimizer = torch.optim.SGD(model.parameters(), lr=0.1)。你需要把模型的参数传给优化器，优化器内部会管理这些参数的指针。
JAX/Optax: optax.sgd 仅仅定义了一套 “梯度变换规则” (Gradient Transformation)。 它不持有任何参数。它只是一个纯粹的函数逻辑：“给我一个梯度，我告诉你参数该怎么变”。

TrainState 本质上是一个 Snapshot (快照) 。它包含了某一时刻训练所需的所有信息。

在 PyTorch 中，训练状态分散在 model (weights) 和 optimizer (momentum buffers) 里。
在 JAX 中，TrainState 就是唯一的真理来源（Single Source of Truth）。输入旧的 State，输出新的 State，这就是训练的本质。

def calculate_loss_acc(state, params, batch):
    data_input, labels = batch
    
    # 1. 前向传播
    # 注意：这里我们显式传递 params。
    # 虽然 state.params 里也有参数，但为了求导，
    # 我们必须把 params 作为一个独立的参数暴露给 jax.grad
    logits = state.apply_fn(params, data_input).squeeze(axis=-1)
    
    # 2. 计算 Loss (Binary Cross Entropy)
    # 使用 logits 而不是 sigmoid 后的概率，是为了数值稳定性 (Numerical Stability)
    loss = optax.sigmoid_binary_cross_entropy(logits, labels).mean()
    
    # 3. 计算 Accuracy (仅用于监控，不参与求导)
    acc = (logits > 0) == labels
    return loss, acc

python

上面定义一个损失函数在Training时会被使用。calculate_loss_acc: 一个计算图函数 $L(w, x)$ 。

Training#

著名的 JAX 训练循环：

State_{t+1} = \text{Update}(State_t, \nabla L(State_t.\text{params}, \text{batch}))

train_step: 灵魂函数 (The Soul of JAX Training)

这是 JAX 区别于 PyTorch 的核心所在。你需要写一个无副作用的纯函数来描述“一步训练”发生了什么。

@jax.jit  # Jit the function for efficiency
def train_step(state, batch):
    # Gradient function
    grad_fn = jax.value_and_grad(calculate_loss_acc,  # Function to calculate the loss
                                 argnums=1,  # Parameters are second argument of the function
                                 has_aux=True  # Function has additional outputs, here accuracy
                                )
    # Determine gradients for current model, parameters and batch
    (loss, acc), grads = grad_fn(state, state.params, batch)
    # Perform parameter update with gradients and optimizer
    state = state.apply_gradients(grads=grads)
    # Return state and any other value we might want
    return state, loss, acc

def train_model(state, data_loader, num_epochs=100):
    for epoch in tqdm(range(num_epochs)):
        for batch in data_loader:
            # 这里的 batch 已经是 NumPy array 了
            # state = 新的 state
            state, loss, acc = train_step(state, batch)
            # 注意：这里不需要手动把数据搬到 GPU，JAX 会自动处理
    return state

trained_model_state = train_model(model_state, train_data_loader, num_epochs=100)

from flax.training import checkpoints
checkpoints.save_checkpoint(ckpt_dir='my_checkpoints/',  # Folder to save checkpoint in
                            target=trained_model_state,  # What to save. To only save parameters, use model_state.params
                            step=100,  # Training step or other metric to save best model on
                            prefix='my_model',  # Checkpoint file name prefix
                            overwrite=True   # Overwrite existing checkpoint files
                           )
loaded_model_state = checkpoints.restore_checkpoint(
                                             ckpt_dir='my_checkpoints/',   # Folder with the checkpoints
                                             target=model_state,   # (optional) matching object to rebuild state in
                                             prefix='my_model'  # Checkpoint file name prefix
                                            )

python

Evaluation#

@jax.jit  # Jit the function for efficiency
def eval_step(state, batch):
    # Determine the accuracy
    _, acc = calculate_loss_acc(state, state.params, batch)
    return acc
test_dataset = XORDataset(size=500, seed=123)
# drop_last -> Don't drop the last batch although it is smaller than 128
test_data_loader = data.DataLoader(test_dataset,
                                   batch_size=128,
                                   shuffle=False,
                                   drop_last=False,
                                   collate_fn=numpy_collate)
def eval_model(state, data_loader):
    all_accs, batch_sizes = [], []
    for batch in data_loader:
        batch_acc = eval_step(state, batch)
        all_accs.append(batch_acc)
        batch_sizes.append(batch[0].shape[0])
    # Weighted average since some batches might be smaller
    acc = sum([a*b for a,b in zip(all_accs, batch_sizes)]) / sum(batch_sizes)
    print(f"Accuracy of the model: {100.0*acc:4.2f}%")
eval_model(trained_model_state, test_data_loader)

python

参数绑定 (Binding)

评估部分除了标准的 eval_step 外，教程还介绍了一个很实用的功能：model.bind。

在训练时，为了配合 jax.grad，我们不得不把参数 params 单独拎出来传来传去：model.apply(params, x)。这写起来很累。

Binding (绑定) 让你可以暂时回归类似 PyTorch 的体验：

# 1. 将训练好的参数 "绑" 回模型结构
trained_model = model.bind(trained_model_state.params)

# 2. 现在你可以像 PyTorch 一样直接调用了！
# 不需要再传 params 了
out = trained_model(data_input)

python

‍

✨ The Fancy Bits ✨#

JAX 的三大神技

自动向量化：jax.vmap (Auto-Vectorization)

这是 JAX 最“魔法”的功能。

痛点：在 PyTorch 中，我们写模型时必须时刻想着 Batch 维度。比如写一个线性层，必须写 x @ w 还要注意维度匹配。
JAX 哲学：只写处理单个样本的逻辑。
- 你定义函数 f(x) 处理形状为 (C, H, W) 的单张图片。
- 调用 vmap(f)，它自动把函数转换成能处理 (B, C, H, W) 的版本。
核心参数 in_axes：
- in_axes=(0, None, None) 是什么意思？
- 假设函数是 simple_linear(x, w, b)。
- 0: 对第一个参数 x，沿着第 0 维进行 Batch 化（每张图不一样）。
- None: 对第二、三个参数 w, b，不进行 Batch 化（所有图共用同一套权重）。
意义：这消灭了复杂的 Batch 维度手动对齐工作，特别是在处理复杂的 Transformer Attention Mask 或高维物理模拟时极为有效。

并行计算：jax.pmap (Parallel Map)

区别：
- vmap 是在单个设备（或逻辑设备）上进行向量化（Vectorization）。
- pmap 是在多个设备（多 GPU/TPU）上进行并行化（Parallelization）。
SPMD 范式：这是 Single Program Multiple Data 的体现。你写一份代码，pmap 把它分发到 8 张卡上同时跑，每张卡处理不同的数据分片。

PyTrees 与 tree_map

定义：JAX 把所有嵌套的容器（List of Dicts, Tuple of Arrays 等）统称为 PyTree。Flax 的 params 就是典型的 PyTree。
工具：
- jax.tree_map(f, tree): 对树里的每一个“叶子节点”（张量）应用函数 f。
- 应用场景：比如你要对所有参数应用 L2 正则化，或者打印所有层的参数形状（如截图所示），不需要写递归循环，一行 tree_map 搞定。

🔪 The Sharp Bits 🔪#

JAX 的“坑”

动态形状 (Dynamic Shapes) —— NLP/Graph 领域的噩梦

问题：JIT 编译是针对特定 Input Shape 特化的。
- 如果你输入 shape (8, 10)，JAX 编译一次。
- 下一次输入 shape (8, 11)，JAX 触发重编译 (Re-compilation) 。
后果：如果你处理 NLP 变长句子，每句话长度都不一样，JAX 就会不停地编译，导致训练极慢。
解决方案：Padding (填充) 。通常把句子 Pad 到固定的 bucket 长度（比如 32, 64, 128），以减少编译次数。

调试 (Debugging)

现象：在 JIT 函数里写 print(x.shape)，它只会在第一次运行（Tracing 阶段）打印出来。真正训练跑了几万次，控制台是静默的。
原因：print 是 Python 副作用，被 JAX Tracer 忽略了。
解决方案：
- 使用 jax.debug.print（教程未提，但这是标准解法）。
- 或者在调试时暂时去掉 @jax.jit。

有状态模块：Dropout 与 BatchNorm (最难理解的部分)

因为 Flax 模型是无状态的，所以遇到本身需要“状态”的层时，处理逻辑会变得很复杂。

Dropout：
- 它在训练时需要随机性。
- JAX 解法：你必须在 apply 时显式传入 RNG Key。

model.apply(params, x, rngs={'dropout': key})

python

并且需要控制开关：deterministic=False (Train) / True (Eval)。

BatchNorm：

痛点：BN 层在训练时需要更新 running_mean 和 running_var。这不是通过梯度更新的，而是直接统计更新的。
JAX 解法：Mutable State。
调用 apply 时，你必须告诉 Flax：“请把 batch_stats 这个集合当作可变的，更新完还给我”。

# 训练时：
logits, new_batch_stats = model.apply(
    {'params': params, 'batch_stats': old_stats}, # 输入旧状态
    x,
    mutable=['batch_stats'] # 声明我们要更新这个
)
# 必须手动保存 new_batch_stats 供下一次迭代使用

python

这是 Flax 劝退新手的最大门槛之一：你必须手动维护非梯度参数的状态流转。