RL01-BC-AIL-ModelBased

主要参考文献： 《模仿学习简明教程》 许天，李子牛，俞杨 NJU&&香港中文大学（深圳）

Introduction

1. 什么是模仿学习？

   1. 核心定义：模仿学习就是从专家示例中学习 。它的目标是让智能体（机器人）能够像人类专家一样进行智能决策。

   2. 为什么需要它？：在通往通用人工智能的道路上，手动编程或设计奖励函数往往非常困难。

      1. 困难点：以自动驾驶为例，要手动把所有约束写出来（比如既要安全不撞车，又要开得平稳舒适）是非常复杂的，很难设计出完美的监督信号。

2. 历史与应用：

   1. 早期案例：早在 20 世纪 80 年代末，CMU 的 Pomerleau 教授就用模仿学习训练出了能横跨北美的自动驾驶车（ALVINN）。
   2. 著名案例：AlphaGo 在击败人类顶尖棋手之前，也使用了模仿学习来学习人类棋谱。
   3. 现代应用：推荐系统、网约车派单系统等，也利用模仿学习来构建虚拟世界，让 AI 在里面试错。

3. 两大算法流派：

   1. BC : 本质上把模仿学习当成回归或分类问题来解。
   2. AIL(Adversarial IL) : 通过逆强化学习 (Inverse Reinforcement Learning, IRL) 的思想。构建一个“对抗的奖赏函数”，然后通过最大化这个奖赏来模仿专家。

4. 适合人群：对模仿学习理论感兴趣，或者希望通过理论分析来改进算法的研究者。

背景介绍

Markov Decision Process

马尔可夫链 (Markov Chain)， 最基础的随机过程：在一个有限的状态集合中，未来的状态只取决于当前的状态，而与过去无关。 $P(s_{t+1}|s_t, s_{t-1}, \dots, s_0) = P(s_{t+1}|s_t)$。

• 状态转移矩阵 (Transition Matrix $P$)

  • 元素含义：$P_{i,j}$ 表示从状态 $i$ 转移到状态 $j$ 的概率。
  • 每一行的和必须为 1（$\sum_{j=1}^{|S|} P_{i,j} = 1$）。这意味着从任何一个状态 $i$ 出发，它下一时刻总得去某个地方（或者留在原地），所有可能去向的概率加起来必须是 100%。

• 轨迹概率的计算 (Trajectory Probability)

  • 目标轨迹 $tr$：$1 \to 2 \to 2 \to 3 \to 1$
  • $P(tr) = P(s_0=1) \times P(1 \to 2) \times P(2 \to 2) \times P(2 \to 3) \times P(3 \to 1)$ (初始概率一般已知，$P(1 \to 2)$：查矩阵第1行第2列，以此类推)

在此基础上加上Action 和 Reward 就变成了 MDP。

1. 动作空间 $\mathcal{A}$：智能体可以采取的动作。
2. 奖励函数 $r$：衡量某一步做得好不好，$r: \mathcal{S} \times \mathcal{A} \to \mathbb{R}$。
3. 状态转移 $P(s_{t+1} | s_t, a_t)$
4. 策略 (Policy) $\pi$ $\pi(a|s)$：表示在状态 $s$ 下选择动作 $a$ 的概率

‍

无限长度的折扣MDP

• 折扣因子 $\gamma$ (Gamma) ： 引入了一个系数 $\gamma \in (0, 1)$。它的作用有两个：

  • 数学上的收敛
  • 重当下轻未来

• 核心目标：累积（期望）回报 $V(\pi)$： 这是衡量一个策略好坏的终极标准

  • $V(\pi) = \mathbb{E} [\sum_{t=0}^{\infty} \gamma^t r(s_t, a_t)]$
  • 有效决策长度：虽然说是“无限长度”，但在数学上，它等效于一个长度为 $H \approx \frac{1}{1-\gamma}$ 的任务 ⁶。这告诉我们，太遥远的未来其实对当前的决策影响微乎其微。

• 两个重要的值函数

  • 状态价值函数 $V^\pi(s)$
  • 状态-动作价值函数 $Q^\pi(s, a)$

对偶表示 (Dual Representation)(这是本教程对模仿学习理论最重要的贡献之一)

状态访问分布 $d^\pi(s)$

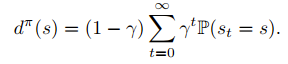
状态-动作访问分布 $d^\pi(s, a)$

为什么这个公式极其重要？

• 它把时间序列的问题（一步步走，算累积奖励），转化成了空间分布的问题（算你在每个状态-动作对上出现的概率）。
• ​对模仿学习的意义：如果我们想让智能体获得和专家一样的回报 $V(\pi) \approx V(\pi^E)$，我们​不需要知道奖励函数 $r(s,a)$ 具体是什么​。我们只需要让智能体的访问分布 $d^\pi(s,a)$ 去逼近专家的访问分布 $d^{\pi^E}(s,a)$。
• 只要两个人的“轨迹分布”重合了，无论奖励函数长什么样，他们拿到的总分一定是一样的。这就是对抗式模仿学习（如 GAIL）的理论基础：状态-动作分布匹配。

‍

有限长度回合制马尔可夫决策过程 (Finite Horizon Episodic MDP)

$H$ (Horizon) ：这是任务的最大时长（或回合长度）。比如一局游戏限制走 100 步，那么 $H=100$。

时变策略-由于环境规则随时间变化，策略也必须随时间变化。

• 策略被定义为 $\pi = \{\pi_1, \dots, \pi_H\}$
• 直观理解：这就像打游戏，开局（$h=1$）的策略可能是“收集资源”，而结尾（$h=H$）的策略可能是“全力攻击”。

$$总分 = \sum (\text{在某时刻某状态做某动作的概率} \times \text{那个时刻那个动作的奖励})$$

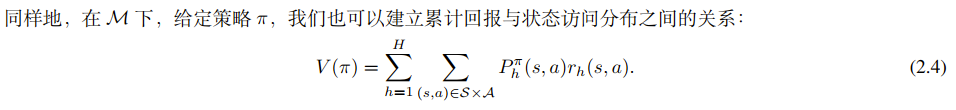
为什么没有折扣因子？

1. 数学上的收敛性无需担心。
2. 在这份教程的理论框架下，“有限长度 MDP”采用的是硬截断（Hard Cutoff） 的方式——在 $H$ 步之内一视同仁（权重为1），$H$ 步之后完全忽略（权重为0）。教程中也提到，无限长度的折扣问题可以通过截断到 $H \approx \frac{1}{1-\gamma}$ 来近似 。这暗示了 **$H$**​ （视野长度） 在这里其实起到了替代 **$\gamma$**​ （折扣因子） 限制“看多远”的作用。

‍

模仿学习问题设定

我们假设存在一个表现不错的专家策略 $\pi^E$。模仿学习的目标是训练一个智能体策略 $\pi$，使得它的累积回报尽可能接近专家。

虽然 RL 和 IL 的目标都是最大化回报，但是条件完全不同：

• ​RL：知道奖励函数，不知道怎么做最好。
• 模仿学习：不知道奖励函数（Reward Function is unknown），但手里有专家数据。

数据形式：专家数据 $\mathcal{D}$ 由 $m$ 条完整的轨迹（Trajectory）组成：$\mathcal{D} = \{tr_i\}_{i=1}^m$ 。每条轨迹包含一连串的状态和动作：$tr = \{s_1, a_1, s_2, a_2, \dots, s_H, a_H\}$。

‍

习题解析

已知环境参数（转移矩阵 $P$ 和奖励 $r$）时，如何算出策略到底好不好（算 $V$）以及智能体爱去哪（算 $d$）。

行为克隆

行为克隆算法

它的核心思想非常朴素：把模仿学习当成一个监督学习（Supervised Learning）问题来做。 也就是：看到专家在某个状态 $s$ 做了动作 $a$，那我就强行记住“在 $s$ 就该做 $a$”。

基本原理 – 最大似然估计（MLE）。

• 我们要找一个策略 $\pi$，让它在看到数据集 $\mathcal{D}$ 里的那些状态 $s$ 时，产生专家动作 $a$ 的概率最大。

  $$\max_{\pi} \sum_{(s,a) \in \mathcal{D}} \log \pi(a|s)$$

  这被称为最大对数似然估计。意思就是：调整我的策略，让我观测到的这堆数据出现的概率最大化。

如果状态空间 $\mathcal{S}$ 和动作空间 $\mathcal{A}$ 都是有限的（比如走迷宫，只有几个格子，只能上下左右），那么最优解非常简单，就是​数数。

$$\hat{\pi}(a|s) = \frac{\text{在数据集里，状态 } s \text{ 下做了动作 } a \text{ 的次数}}{\text{在数据集里，状态 } s \text{ 出现的总次数}}$$

• 没见过的状态怎么办？
  如果遇到一个状态 $s$ 是专家没去过的，教程建议使用均匀分布（瞎猜），即 $\pi(a|s) = \frac{1}{|\mathcal{A}|}$

• 最大化似然度（MLE）在数学上等价于最小化策略分布之间的差异（KL 散度）。也就是我们在强行把我们的策略分布 $\pi$ 拉向专家的分布 $\pi_E$。

‍

参数化方法 (针对连续/复杂空间)

在现实世界（如自动驾驶、机器人控制）中，状态往往是连续的（比如摄像头的像素、激光雷达的数值），我们不可能通过“查表数数”来解决，因为你几乎永远不会遇到两个完全一模一样的像素值。

这时，我们需要用函数近似（Function Approximation），比如神经网络，来表示策略 $\pi_\theta$。目标函数转化为 公式 ：

$$\max_\theta \sum_{(s,a) \in \mathcal{D}} \log (\hat{\pi}_\theta(a|s))$$

例题 3.1：Softmax 参数化（对应“分类问题”）

• ​场景：动作是离散的（如：左转、右转、刹车）。
• ​做法​：神经网络输出一个向量，通过 Softmax 函数归一化成概率。
• ​本质​：这时候的优化目标，就是大家熟悉的分类任务里的​交叉熵损失函数 (Cross-Entropy Loss) 。

例题 3.2：Gaussian 参数化（对应“回归问题”）

• ​场景：动作是连续的数值（如：方向盘转动 23.5 度）。

• 做法：假设策略服从高斯分布（正态分布）。神经网络预测高斯的均值 $\mu_\theta(s)$。
  如果我们假设高斯分布的方差 $\sigma^2$ 是个常数，那么最大化高斯分布的对数似然，数学上等价于：

  $$\min_\theta \sum_{(s,a) \in \mathcal{D}} (a - \mu_\theta(s))^2$$

• ​本质​：这就是最经典的​均方误差 (MSE) 回归。

‍

总结：

• 如果动作是离散的 $\to$ 做​分类 (Classification) 。
• 如果动作是连续的 $\to$ 做​回归 (Regression) 。

复合误差

复合误差 (Compounding Error) 是模仿学习理论中最著名的概念之一，它揭示了行为克隆（BC）算法最大的“死穴”。

简单来说：一步错，步步错，最终满盘皆输。

教程引用了自动驾驶先驱 Pomerleau 的经典观察：

• ​训练时：神经网络使用的是专家数据，专家开车很稳，总是在路中间，所以数据集中全是“在路中间如何微调”的样本。
• ​测试时​：神经网络自己开车。如果它犯了一个小错误（比如偏离了路中心 10 厘米），它就进入了一个​训练集中从未出现过的状态（专家从没开偏过）。
• ​后果​：在未见过的状态下，神经网络可能不知所措，做出随机或错误的动作，导致车偏离得更远（比如偏离 1 米）。错误像滚雪球一样越来越大，直到撞车 ¹。

数学解释：分布漂移 (Distribution Shift)

• ​问题的根源：

  • 训练数据来自专家策略 $\pi^E$ 产生的状态分布 $d^{\pi^E}$。
  • 测试/评估数据来自学习到的策略 $\hat{\pi}$ 产生的状态分布 $d^{\hat{\pi}}$。
  • 因为 $\hat{\pi}$ 不可能完美复制 $\pi^E$，所以这两个分布是不一样的。

误差上界平方级别增加。

**为什么是平方级 (​$H^2$**​ )？

• 一个 $H$ 来自于你做错了动作，当步的奖励丢了，并且影响了后面所有的步（失去了 $H$ 个奖励）。

样本复杂度回答了“到底需要多少专家数据才能学好”的问题。

• ​结论：在最坏情况下，需要的样本量 $m$ 与 $H^2$ 成正比。

  • 无限长度：$m \approx O(\frac{|\mathcal{S}|}{(1-\gamma)^2 \epsilon})$ 。
  • 有限长度：$m \approx O(\frac{H^2 |\mathcal{S}|}{\epsilon})$ 。

• 极小极大最优 (Minimax Optimal)：
  教程中有一个非常重要的笔记指出：虽然 $H^2$ 的误差看起来很糟糕，但在不知道环境转移概率（即不知道世界怎么运作）的情况下，行为克隆 (BC) 已经是我们能做到的最好的算法了 。这说明 $H^2$ 的误差是这一类问题的固有难度，而不是算法设计得烂。

简单的行为克隆（BC） 虽然好用，但在长序列决策中非常脆弱。

DAgger

DAgger 全称是 Dataset Aggregation（数据集聚合） 。它的核心思想是：把“离线学习”变成“在线学习”，主动去问专家在那些陌生的状态下该怎么做。

每一次迭代循环： 混合策略 --> 收集数据 --> 专家标注 --> 聚合数据 --> 重新训练

为什么它能解决复合误差？ BC 失败是因为它没见过“跑偏”的状态。DAgger 强行让智能体去环境里“试错”，一旦跑偏，马上请专家打标签。这样，智能体就学会了如何从错误状态（跑偏）回到正确状态（路中心） ，从而消除了复合误差。

Debate

• 为 BC 辩护： 虽然 BC 有复合误差，但这不是算法的问题，是命题的问题。如果只给你一个固定的数据集（不准交互），从信息论的角度可以证明，任何算法在最坏情况下都会有复合误差。所以 BC 其实在它的设定下已经做得很好了。

• 对 DAgger 的冷静分析：DAgger 看起来很美好，因为它改变了题目设定（允许与环境交互+咨询专家）。

  但是，理论分析表明，DAgger 未必比 BC 省样本。

  • ​原因：智能体一开始是瞎走的，它探索到的状态分布可能和专家真实的分布相差十万八千里。
  • 结论：为了达到同样的精度（$\epsilon$-最优），DAgger 需要咨询专家的总次数，在最坏情况下，可能并不比 BC 需要的样本量少 。

• ​DAgger 的本质​：通过​人机回环（Human-in-the-loop） ，不断把智能体跑偏的那些“边缘情况（Corner Cases）”抓回来让专家重新教，从而增强系统的鲁棒性。

• ​理论地位：DAgger 是工程上解决复合误差的有效手段，但在统计效率（样本复杂度）上，它并没有打破理论的上限。

对抗式模仿学习

个人talking – 这一章的学习价值

在目前的端到端自动驾驶（如 Tesla FSD V12 路线）和具身智能操作（如 Diffusion Policy, ACT 等）的主流落地中，简单的 Behavior Cloning (BC) 及其变体（配合 Transformer/Diffusion）占据了统治地位。

为什么AIL现在 “销声匿迹” 了？

在工业界和应用导向的研究中，对抗式模仿学习（AIL）确实面临几个痛点，导致它不如 BC 流行：

• 训练极不稳定：AIL（特别是 GAIL）借鉴了 GAN 的思路，是一个极小极大（Minimax）优化问题 。这意味着你需要同时训练一个判别器（Reward）和一个策略（Policy），很难调参，很难收敛。相比之下，BC 只是一个稳定的监督学习（回归/分类）。
• 采样效率低：AIL 本质上是在做强化学习（RL），需要智能体与环境进行大量交互 。在真机机器人或自动驾驶中，通过“试错”来学习太昂贵、太危险。
• BC 变强了：随着 Transformer 和 Diffusion Model 的引入，BC 对多模态分布的拟合能力大幅增强，掩盖了它在理论上的部分缺陷（复合误差）。

但如果想做Post-Training RL（训练后强化学习）或者深入理解为什么 BC 会失效，这一章包含非常关键的理论视角：

• 理解BC的理论天花板(State-Action Distribution Matching)

• Post Training RL的基本石（Reward 也是学出来的）：

  • 现在的具身智能前沿（如 VLA 模型）开始探索 Post-Training 阶段。在这个阶段，单纯的 BC 已经不够了，我们需要 RL 来进一步微调模型。
  • Reward 从哪来？ 在精细装配等任务中，很难手工写出完美的 Reward 函数。
  • AIL 的启示：AIL 的核心思想就是逆强化学习（IRL） ——让判别器充当 Reward Function。
  • 连接：目前的很多前沿工作（如利用人类反馈、利用 VLM 打分）本质上都是在构建一个“判别器”或“奖励模型”，然后用 RL 去优化。这正是这一章讲的 “极小极大优化建模” 的思想。

• TAIL 和 MIMIC-MD 算法，展示了如何结合 BC 的优势（利用数据）和 AIL 的优势（利用环境模型）

  • TAIL 的核心是利用环境的转移概率信息来辅助模仿 --> 现在的变体 World Models (世界模型) Based RL
  • MIMIC-MD 的核心思想是：只在数据集覆盖的状态上模仿专家，别的地方不要瞎猜 --> 现代变体：Offline RL (离线强化学习) 中的“保守主义” 在 Post-Training RL 中，我们最怕模型在没见过的数据上乱动（OOD Action）。现代算法通过正则化项来惩罚偏离数据集分布的行为。–> CQL (Conservative Q-Learning) , IQL (Implicit Q-Learning) 。
  • 现在倾向于使用 DPO，RL-VLM-F。

所以这章的学习对我而言是轻推导重理论思想的。

状态动作分布匹配

• 出发点：回顾之前的对偶公式：$V(\pi) = \sum \sum P_h^\pi(s,a) r_h(s,a)$。只要模仿策略的状态-动作访问分布 $P_h^\pi$ 和专家的分布 $P_h^{\pi^E}$ 长得一样，那么无论奖励函数 $r$ 是什么，它们得出的总分 $V(\pi)$ 一定是一样的,即奖励无关性。

  • “既然模仿学习不知道真实的奖励函数 $r$，你怎么敢保证你学出来的策略也是高分的？”
  • 与其学习策略，不如直接匹配分布。

• 新的目标函数 ：因此，AIL 的目标不再是最小化动作误差，而是最小化两个分布之间的距离：

  $$\min_{\pi \in \Pi} \sum_{h=1}^H \psi(P_h^\pi, P_h^{\pi^E})$$

  其中 $\psi$ 是某种距离度量（比如后面会用到的 TV 距离或 JS 散度）。

教程再次利用 Reset Cliff 环境来对比两种准则，这是理解 AIL 优势的关键：

• BC 的准则（ 策略分布匹配 ）：
  BC 关注的是 $\pi(a|s)$。在没见过的数据（未访问状态）上，BC 倾向于瞎猜（均匀分布）。在 Reset Cliff 中，这意味着它有概率走到坏状态 $b$ 并掉下去，导致复合误差。

• AIL 的准则（ 状态-动作分布匹配 ）：AIL 关注的是 $P(s,a)$。

  • 专家的数据显示：在坏状态 $b$ 上的访问概率是 ​0（$P_h^{\pi^E}(b, \cdot) = 0$）。
  • 为了让两个分布匹配，AIL 强迫智能体的策略​也不能访问状态 $b$。
  • ​结果：智能体为了不让 $P(b)$ 变成正数，会主动学会避开那些通往 $b$ 的路，即使在数据集中没见过这些具体的动作。这就在根本上避免了复合误差。

虽然理念很美好，但在实际操作中，我们并没有上帝视角拿到真实的专家分布 $P_h^{\pi^E}$，我们只有一堆离散的数据点 $\mathcal{D}$。

• 最大似然估计 (MLE)：我们只能用“数数”的方法来估计专家的分布 $\hat{P}_h^{\pi^E}$。

• 定理 4.1 (反直觉的样本复杂度)：如果我们用 TV 距离（Total Variation Distance）作为度量标准来优化，需要的专家样本量 $m$ 是多少？

  • ​结论：$m \gtrsim \frac{H^2 |\mathcal{S}|}{\epsilon^2}$。
  • ​对比：之前 BC 的样本复杂度是 $\tilde{O}(1/\epsilon)$，而这里是 $\tilde{O}(1/\epsilon^2)$。
  • 这意味着什么？ 当我们要求精度很高（$\epsilon$ 很小）时，比如 $\epsilon=0.01$，BC 可能只需要 100 个数据，而 AIL 可能需要 10000 个数据！

• 原因分析： 这并不是因为 AIL 的策略差，而是因为统计估计太难了。 我们要从有限的数据中估计出一个完美的概率分布 $\hat{P}_h^{\pi^E}$，这个估计过程本身的误差收敛速度很慢（速率为 $O(\sqrt{1/m})$），从而拖累了整个算法的样本效率。

小总结：

• 好消息：从机理上讲，状态-动作分布匹配（AIL）比BC更高级，因为它能通过“拒绝访问坏状态”来自动修正复合误差。
• ​坏消息​：从统计上讲，​直接做分布匹配非常昂贵。因为仅仅通过有限的样本去还原一个高维分布是非常困难的，这导致传统的 AIL 算法（如 GAIL, FEM）在最坏情况下的样本效率其实不如 BC。

极小极大优化建模

原始目标：我们的理想是直接最小化模仿策略 $\pi$ 和专家 $\pi^E$ 之间的距离（比如 TV 距离）：

$$\min_{\pi} D_{TV}(P^\pi, P^{\pi^E}) = \frac{1}{2} \sum |P^\pi - P^{\pi^E}|$$

你很难直接告诉神经网络，概率分布往哪里改一点点，好让积分距离变小。

解决方案：对偶表示 (Dual Representation) 数学上，$L_1$ 范数（TV 距离对应 $L_1$）有一个“对偶形式”。利用这个性质，我们可以把“最小化距离”转化为一个极小极大（Minimax） 问题

$$\min_{\pi} \max_{w} \sum w(s,a) (\hat{P}^{\pi^E}(s,a) - P^\pi(s,a))$$

• $w$ 就是奖赏函数 (Reward Function) ：如果我们把 $w$ 看作奖励，那么 $\sum w(s,a) P(s,a)$ 其实就是策略在 $w$ 下的累积回报 $V_w$。

• However，这里的 $w$ 其实是一个第一层逻辑里说的那个“真实奖励 $r$”。它是依据对偶公式制造出来的 “Fake Reward” 。

  • 真实奖励 $r$：代表任务的终极目标（比如“把螺丝拧紧”）。
  • 对抗奖励 $w$：代表两个分布目前的差异程度（比如“你现在的姿势和专家不太像”）。

对抗博弈的目标：

$$\min_{\pi} \max_{w} (V_w(\pi^E) - V_w(\pi))$$

• 内层循环 ($\max_w$) ：$w$ 的身份 GAN 里的判别器。 它的目的是找茬，它要设计一套奖励规则，使得专家得分很高，而你（智能体）得分很低 ，从而最大化你们之间的差距 。
• 外层循环 ($\min_\pi$) ：$\pi$ 的身份是 “学生”（生成器） 。它的目的是在考官制定的规则下，努力拿高分，从而最小化和专家的差距 。

怎么训练？梯度下降-上升 (Gradient Descent Ascent)

• Step 1: 优化考官 $w$ (上升)

  • 目标是让专家和策略的分布差异在 $w$ 的加权下最大化。
  • 使用在线投影梯度下降（因为 $w$ 有范围限制 $||w||_\infty \le 1$）。

• Step 2: 优化学生 $\pi$ (下降/RL)

  • 目标是最大化这个 Reward 下的回报 $V_w(\pi)$。
  • 这本质上就是强化学习！ 我们可以直接调用任何标准的 RL 算法（如策略梯度 PG、TRPO、PPO 等）来更新 $\pi$。

都是在解同一个极小极大优化问题，区别只在于 “怎么定义距离” 以及 “怎么更新参数” 。

维度	FEM (特征期望匹配)	GTAL (博弈论学徒学习)	GAIL (生成对抗模仿学习)
1. 特征定义 ($\phi$) (核心区别)	人工设计 / 已知 (Linear Features)	人工设计 / 已知 (Linear Features)	自动学习 / 隐式 (由神经网络判别器$D$提取)
2. 对应距离 ($\psi$) (优化目标)	$L_2$​范数 (欧氏距离)	$L_\infty$​范数 (最大范数/切比雪夫距离)	JS 散度 (Jensen-Shannon Divergence)
3. 奖赏函数$w$的约束 (对偶空间的形状)	$L_2$​球 ( $||w||_2$ )	$L_1$​球 / 单纯形 ($||w||_1$)	隐式约束 (由判别器网络架构决定)
4. 奖赏函数$w$的更新 (对抗者怎么找茬)	残差计算 (直接计算特征差值:$\hat{P}^E - P^\pi$)	镜像下降 (指数乘法更新:$w \cdot \exp(\dots)$)	梯度上升 (训练二分类判别器)
5. 策略$\pi$的更新 (学习者怎么改进)	混合分布 + 线搜索 (寻找步长$\eta$混合新旧分布)	标准 MDP 规划 (求解当前$w$下的最优策略)	策略梯度 (RL) (如 TRPO/PPO 更新神经网络)

GAIL是GAN在RL领域的转型，本质是IL算法，但是在策略更新阶段使用RL，奖励信号来自奖赏函数​$w$。

以上是跳过历史直接得出的直观结论，接下来我讲回顾一下 学徒学习 和 对抗模仿学习 是如何统一的。

• ​旧派 (FEM/GTAL) ​：觉得我在匹配​特征期望（比如“专家这一局吃了10个苹果”，我也要吃10个）。
• ​新派 (GAIL) ​：觉得我在匹配​概率分布（比如“专家在坐标(10,10)出现的概率是0.5”，我也要是0.5）。

大家后来证明了： “分布”其实就是一种极致细腻的“特征”。

更高级的对抗模仿学习算法

虽然 AIL 策略更稳健，但在 “最坏情况（Worst-Case）” 下，经典的 AIL 算法（如 GAIL、FEM）所需的样本复杂度并不比简单的 BC 好，甚至可能更差（BC 是 $1/\epsilon$，而 AIL 往往是 $1/\epsilon^2$）。

• 潜台词：AIL 虽然方向对，但样本效率太低，需要太多的专家数据。

在本小节，我们假设算法已知环境的转移概率并且专家策略是一个确定性策略。

​TAIL

分布分解公式 (4.9)：

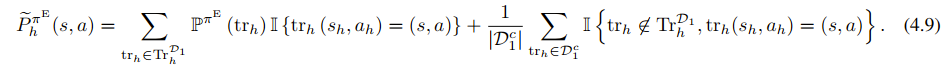
TAIL 把专家分布 $\tilde{P}$ 拆成了两部分来估计：

1. ​第一部分（算出来的） ：对于那些在 $\mathcal{D}_1$ 中完全被覆盖的轨迹，我们不需要估计！因为我们知道转移概率 $P(s'|s,a)$，我们可以精确计算出它们发生的概率。这一部分误差为 0。
2. ​第二部分（估计出来的） ：只有那些“跑偏了”或者“没见过”的稀有轨迹（在 $\mathcal{D}_1$ 之外），我们才被迫用 $\mathcal{D}_1^c$ 的数据去进行统计估计。

• ​初始化：切分数据，构造好那个聪明的估计器 $\tilde{P}_h^{\pi^E}$。

• ​循环迭代：

  • ​求策略 $\pi^{(t)}$：在当前奖励 $w^{(t)}$ 下，解 MDP 得到最优策略（因为假设已知环境模型，这一步比较容易）。
  • ​算分布：算出当前策略的分布 $P^{\pi^{(t)}}$。
  • ​更奖励 $w^{(t+1)}$：对比 $\tilde{P}^{\pi^E}$（聪明的估计）和 $P^{\pi^{(t)}}$（当前的策略），更新奖励函数来拉大差距。

• ​输出：输出所有历史策略的平均混合策略。

在对抗模仿学习中，与其盲目地从数据中估计专家分布，不如利用环境模型（Transition）先精确计算出能算的部分，只估计算不出来的部分。 这种混合估计策略显著降低了方差，提升了学习效率。

​MIMIC-MD​MIMIC-Mixture Distribution（模仿-混合分布）

这个算法的核心哲学是：​ “守正出奇” 。

• ​守正：在见过的地方，一定要和专家一模一样（Behavior Cloning）。
• 出奇：在没见过的地方，利用环境模型来规划，尽量不要跑偏（Distribution Matching）。

1. 核心设定：强行模仿 (Constraints)。MIMIC-MD 比之前的 TAIL 算法更“保守”。它首先定义了一个策略集合 $\Pi_{mimic}(\mathcal{D})$：

$$\Pi_{mimic}(\mathcal{D}) = \{ \pi \mid \forall s \in \mathcal{D}, \pi(s) = \pi^E(s) \}$$

2. 优化目标：

它的思想启发了后来的许多保守离线强化学习（Conservative Offline RL） 算法。

‍

• ​TAIL：基于梯度下降-上升（GDA），类似于训练神经网络。
• MIMIC-MD：基于线性规划 (Linear Programming) 。因为它的约束是硬性的，且目标函数是线性的，所以可以转化为一个巨大的 LP 问题在多项式时间内求解。
• TAIL处理数据噪声能力或者非确定性策略表现时可能表现更好。

Debate

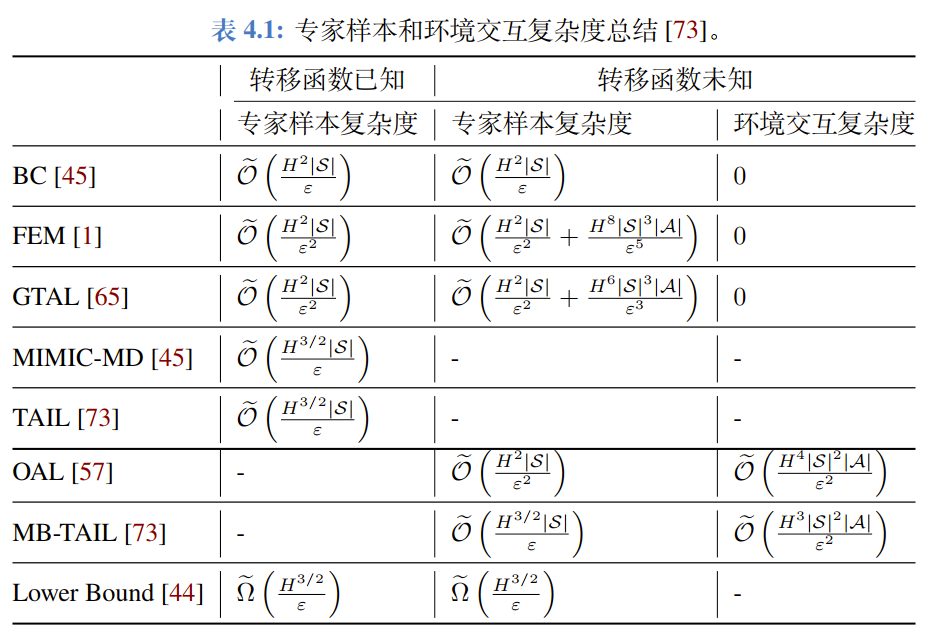
看图的诀窍：看斜率

教程给出了一个非常有用的公式：

$$\log(\text{Gap}) \approx -\frac{1}{\beta} \log(m) + \text{const}$$

这意味着在双对数坐标系下，Policy Value Gap 随样本量 $m$ 变化的曲线斜率，直接反映了算法的阶数 $\beta$。

• 如果斜率是 -1，说明 $\beta=1$，误差是 $O(1/m)$ 级别的（快）。
• 如果斜率是 -0.5，说明 $\beta=2$，误差是 $O(1/\sqrt{m})$ 级别的（慢）。

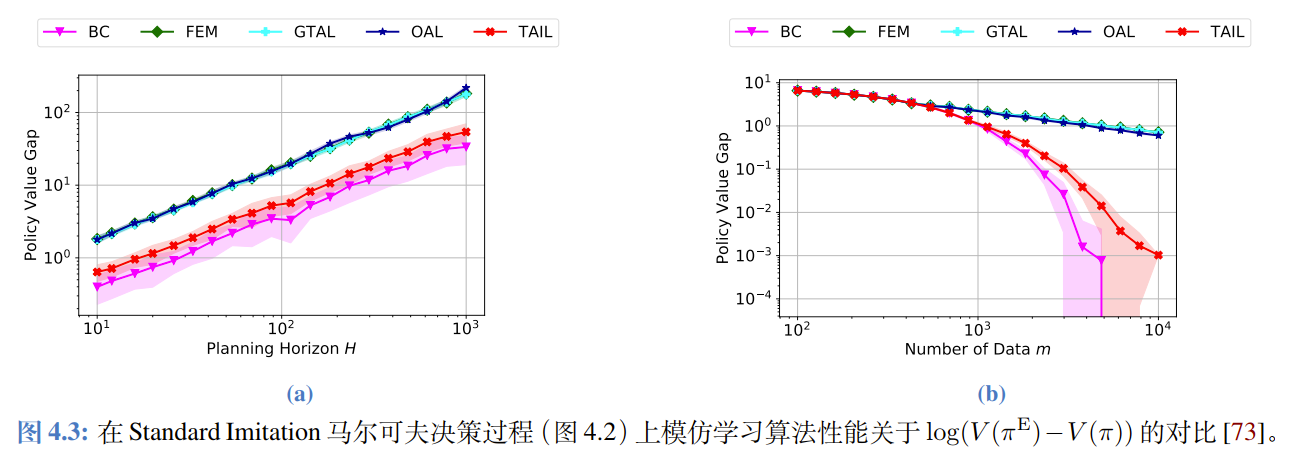
• ​BC 和 TAIL：红线和粉线掉得很快，斜率接近 -1。说明它们充分利用了数据，收敛快。
• ​FEM/GTAL/OAL：蓝线和青线掉得很慢，斜率接近 -0.5。说明它们受困于统计估计的低效，收敛慢。
• ​结论：实验完美验证了理论——TAIL 通过利用“缺失质量（Missing Mass）”性质，成功修正了传统 AIL 的统计缺陷，达到了和 BC 一样的样本效率。

环境模仿

环境模仿学习

学习近似的Reward和Transition Function。

• 经验模型 $\hat{\mathcal{M}}$ 的组成，包含三个核心要素的近似值：

  • $\hat{r}$：近似的奖赏函数。
  • $\hat{P}$：近似的转移函数。
  • $\hat{\rho}$：近似的初始状态分布。

• 好处：
  极大地降低了真实环境的样本复杂度。因为在虚拟模型里采样是免费且安全的，而在真实世界（比如真车、真机器人）里试错是昂贵且危险的。

• 真实交互 (Sampling)
• 模型训练 (Model Learning)：监督学习
• 策略优化 (Policy Optimization)：目标是最大化虚拟世界里的回报 $V_{\hat{\mathcal{M}}}^\pi$。
• 循环：策略变强了，再去真实世界收集更难的数据，回来更新模型，周而复始。

把“构建环境模型”这件事，看作是一种“模仿学习”。

• ​困难模式：模仿转移函数 $\hat{P}$。

  • 这是一个高维的条件概率分布。特别是当状态空间很大（比如图像）时，预测“下一帧会发生什么”是非常困难的。

基于行为克隆的环境模仿学习

对偶智能体（环境） ：输入状态-动作对 $(s, a)$，输出下一个状态 $s'$。

算法实现：MLE

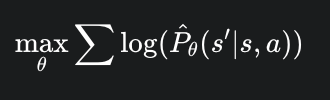
在虚拟环境里推演未来时，你是用预测出来的 $s_{t+1}$ 去预测 $s_{t+2}$，再预测 $s_{t+3}$……模型只要在 $t=1$ 时有一点点误差，这个误差就会在后续的时间步里不断累积、放大，导致预测 100 步之后的世界和真实世界面目全非。

基于对抗式的环境模仿学习

• ​建模变化：

  • 之前的策略模仿：我们匹配的是状态-动作分布 $d^\pi(s, a)$。
  • 现在的环境模仿：我们需要匹配状态-动作-下一状态分布 $d^\pi(s, a, s')$。

• ​直观理解：

  • 判别器（Discriminator）现在要看三个东西 $(s, a, s')$。
  • 它的任务是分辨：这个跳转 $(s \to s')$ 是真实物理世界发生的（Real），还是虚拟环境模型模拟出来的（Fake）？
  • 环境模型（Generator）的目标是生成极其逼真的 $s'$，骗过判别器。

它证明了如果我们用对抗训练（GAIL）的方法去学习环境模型，在进行策略评估时，误差随时间步的增长是线性的，而不是二次方的。但是依然存在样本效率降低的问题。

总结

• ​出发点​：从统计学的角度揭示模仿学习的本质。
• ​问题​：揭示了行为克隆 (BC) 的复合误差来源。
• ​解决​：介绍了对抗式模仿学习 (AIL) 如何通过分布匹配缓解复合误差。
• ​反转​：指出了传统 AIL 的​统计缺陷​（样本效率低），并介绍了 TAIL/MIMIC-MD 等新方法如何克服这一难题。
• 拓展：最后将思路应用到了环境模仿（构建虚拟世界）中。

‍

​五个“未完成”的主题

1. 深度学习理论 (Non-finite State/Action Spaces)

   1. 内容：当状态和动作无限（如连续控制、图像输入）时，我们必须用神经网络(Transformer)做函数近似。这时除了统计问题，还有非凸全局优化的问题。

2. AggreVaTe 算法族

   1. 内容：除了 DAgger，还有一类基于 “Aggregate Values to Imitate” 的在线学习算法。利用价值函数来指导数据聚合。

3. ⭐ 模仿与强化的结合 (IL + RL)

   1. 内容：在很多任务中，给定的专家策略可能不是最优的（例如人类操作不够完美，或者遥操作有噪声）。这时模仿学习只是 “铺垫” （Initialization/Warm-start），后续需要接强化学习来超越专家。
   2. 建议：可以去查阅文中标注的参考文献 [13, 23, 38, 60]，看看前人是如何从 IL 平滑过渡到 RL 的。

4. VTR 类环境模仿 (Value-Targeted Regression)

   1. 内容：另一种构建环境模型的方法。它的目标不是让 $\hat{P}$ 预测得准，而是直接最小化 “估计的值函数与真实值函数的差异” 。
   2. 关联： 这是 Model-based RL 的一种高级形式，关注​ “有用的预测” ​而不是“准确的预测”。

5. ⭐ 探索问题 (Exploration)

   1. 内容：对抗式模仿学习需要不断与环境交互。如何在学习过程中 平衡探索（尝试新动作 和 利用（模仿专家） 是一个核心难题。当然现在也有“Beyond探索利用”的工作，这个地方还存在争议。

祝贺您啃完了这块理论硬骨头！ 有了这些理论打底，再看现在的 Diffusion Policy 或 OpenVLA 的论文，您会更容易看透它们是在解决什么本质问题（是解决分布偏移，还是解决样本效率）。再看一些MBRL以及Offline RL工作里面的一些方法，你也会发现很多东西都不是新东西。

‍